 |
April 19 - 23, 1999
ABSTRACTS
Monday, April 19, 1999
Symposium on Numerical Stochastics in Finance
Phelim P. Boyle
Introduction to Modern Finance
In the the last 20 years there has been an explosive growth in financial innovation
and the development of new financial markets. There are many reasons for this
including advances in technology, deregulation and new breakthroughs in academic
research. In this talk we discuss the basic ideas in modern finance staring
with brief institutional details followed by a discussion of some of the key
concepts. We will use a simple securities market model to illustrate the concepts
of no arbitrage and incomplete markets and develop the connection between
no arbitrage and the existence of an equivalent martingale measure. For the
most part we will work in discrete time occasionally alluding to the continuous
time formulation. We will contrast the no arbitrage approach with the equilibrium
approach and discuss the valuation of new securities in an incomplete market.
We will explore issue in valuation and hedging and indicate applications of
the Monte Carlo method to exotic options and the estimation of portfolio risk.
We will also discuss the famous (or infamous!) Value at Risk concept and mention
some of the challenges it presents. We will mention the problem of valuation
of American options in high dimensions and briefly outline the progress attained.
The talk will assume little background by way of finance knowledge.
Pierre L'Ecuyer
Monte Carlo and Quasi-Monte Carlo Methods
The talk will discuss Monte Carlo and quasi-Monte carlo methods and give examples
of their application in finance. Efficiency improvement techniques such as
common random numbers, control variates, stratification, conditional Monte
Carlo, and importance sampling, will be explained. The construction of random
number generators, the philosophy behind, and their quality criteria will
be discussed. Low-discrepancy point sets and sequences, such as lattice rules,
nets, and randomized versions of them, will be covered. Concrete examples
from finance, with numerical results, will be given.
Dietmar Leisen
Continuous-Time Finance and Its Approximations
This talk discusses pricing and hedging in continuous time and practical
implementations to calculate prices in asset market models. We start with
a financial model where prices follow geometric Brownian motion (Black-Scholes
model). We discuss Girsanov's theorem, the Feynman-Kac representation of prices
as expectations and the Black-Scholes PDE. We do then discuss lattice approximations
and the specific numerical difficulties, which arise: convergence issues,
order of convergence, and possible improvements. We also study incomplete
markets and generalize the model in several directions: one-dimensional diffusions,
multinomial diffusions, jump-diffusions and stochastic volatility models.
Philip Protter
Numerical Methods for Stochastic Differential Equations arising in Finance
A standard problem in Finance Theory is to price derivatives and
to estimate hedging strategies. The simple Black-Scholes paradigm gives rise
often to formulas which are explicit or involve solutions of PDEs. If one
leaves the realm of modeling security prices with linear SDEs, however, and
uses non linear coefficients, then the usual methods break down, and one must
rely on simulations of the solutions of SDEs combined with Monte Carlo techniques.
We will focus on the problem of pricing of derivatives, however the hedging
problems can be handled similarly. We discuss recent attempts to mathematically
analyze this type of procedure: for example if we use an Euler scheme for
the SDE and combine it with a Monte Carlo scheme, what is the error? How should
the step size of the Euler scheme be related to the number of simulation?
We then discuss the situation when the paradigm is further generalized to
include jumps. This leads to complete models through the Azema martingales,
and to incomplete models via (eg) Levy differentials. In the latter case the
mathematical analysis is just beginning and some simulation problems arise.
Tuesday, April 20, 1999 - Friday, April 23, 1999
Workshop on Numerical Methods and Stochastics
Dan Crisan
Numerical methods for solving the stochastic filtering problem
We present a survey of existing approaches to solve numerically
the stochastic filtering problem: linearisation methods (extended Kalman filter),
approximation by finite dimensional non-linear filters, particle filters,
classical partial differential equations methods, Wiener Chaos expansions,
moment methods. We explain some of the differences between these methods and
make a few comparative remarks.
Optimal filtering on binary trees
The stochastic filtering problem is stated for signal processes evolving on
discrete sets, in particular on binary trees. Approximating algorithms for
generating the posterior distribution of the signal are introduced and optimality
results regarding the mean relative entropy of the approximating measure with
respect to the posterior measure are presented.
Pierre Del Moral
Genetic/particle algorithms and their application to integration of functionals
in high dimensions
The talk will survey the applications of methods arising in the
study of interacting particly systems, and in genetic models, to problems
of approximating various high-dimensional integrals.
Branching and Interacting Particle Systems Approximations of Feynman-Kac Formulae
with Applications to Non Linear Filtering
This talk focuses on interacting particle system methods for the numerical
solving of a class of Feynman-Kac formulae arising in the study of certain
parabolic differential equations, physics, non linear filtering and elsewhere.
We will give an expos\'e of the mathematical theory that may be useful in
analyzing the convergence of such particle approximating models including
law of large numbers, large deviations principles, fluctuations and empirical
process theory as well as semi-group techniques and limit theorems for processes.
In addition, we will investigate the delicate and probably the most
important problem of the long time behavior of such interacting measure valued
processes. We will show how to connect this problem with the asymptotic stability
of the corresponding limiting process so that to derive useful uniform convergence
results with respect to the time parameter.
Jessica Gaines
Discretisation methods for numerical solution of SDE's and SPDE'S
After a brief reminder of the use of discretization schemes for approximation
of (mainly pathwise) solutions of stochastic differential equations, the
talk will review work to date on numerical solution of stcohastic partial
differential equations (SPDE's). Both finite difference and finite element
methods will be covered. Most work has been done on parabolic equations,
but there are also some initial results and/or experiments involving the
solution of elliptic and hyperbolic SPDE's.
Optimal convergence rates of discretisation methods for parabolic SPDE's
We answer the question "What is the best rate of convergence obtainable
when solving the parabolic SPDE
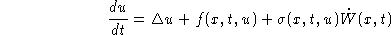
using a finite difference method in a certain class?" Gyöngy showed
that the most obvious method has rate of convergence with .
Can one do better than this? If so, how?
Alice Guionnet
Particle systems approximations of non-linear differential equations I
Particle systems approximations of non-linear differential equations II
We shall review some examples where particle methods are used to approximate
physical quantities, such as solutions to non-linear differential equations
of non-linear stochastic differential equations. We shall analyze convergence,
large deviations, and central limit theorems for such approximations. Applications
to non-linear filtering problems will also be given.
Terry Lyons
Mathematical problems in numerical stochastic analysis
This talk is intended to be informal, and to set out a series of questions
and connections in the scientific computation of stochastic systems. The
aim is to expose problems where mathematical progress would yield benefit.
Rough paths and variable steps in the numerical analysis of fractional and
classical stochastic processes
Rough Paths give a new way of approximating the underlying noise in many
stochastic systens. This can be exploited in new algorithms.
Laurent Miclo
Time-continuous interacting particle approximations of Feynman-Kac formulae
We will present a weighted sampling Moran particle system model for the
numerical solving of the Feynman-Kac formulae appearing, among others, in
the non-linear filtering equations. Up to some classical transformations,
the latter can also be seen as a simple (but time-inhomogeneous and in a
random environment given by the observations) generalized spatially homogeneous
Boltzmann equation, so our general continuous time approximation is also
related to the corresponding Nanbu-type interacting particle systems. But
we will develop a new proof rather based on martingales and semigroup techniques
to prove the convergence when the number of particles increases with an
upper bound on the speed of convergence which is typical of the propagation
of chaos. We also establish a functional central limit theorem for the fluctuations,
and under some mixing assumptions, we will get uniform convergence results
with respect to the time parameter.
Philip Protter
S ome recent results concerning numerical methods for stochastic differential
equations
We will survey some numerical techniques used to analyze stochastic differential
equations, and recent theorems concerning the mathematical analysis of such
techniques. For example if one uses an Euler scheme to approximate a solution
of an SDE, one can describe the asymptotic normalized error. Then if one
adds a Monte Carlo approximation to evaluate a function of the solution,
one can analyze the asymptotic normalized error of the entire solution.
This reveals the interplay between the number of simulations and the partition
step size. We will then discuss new directions of research for numerical
methods: non Brownian models such as SDEs driven by Levy processes; functionals
of the paths of the solutions instead of simply functions of the paths;
forward-backward equations; and backward equations. This is a research area
in its infancy.
Frederi Viens
Simulating the fast dynamo problem for stochastic magneto-hydrodynamics via
discretized Feynman-Kac formulae
In a viscous magnetic fluid with given velocity field, the magnetic field
H is a 3d-vector-valued random field on 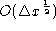 (or a domain of
(or a domain of 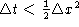 ) which
satisfies a linear system of parabolic partial differential equations. If
the velocity field is assumed to be white-noise in time and smooth in space,
then H will satisfy a linear system of three stochastic PDEs, in which the
zero- and first-order terms have coefficients that are white-noise in time.
It is conjectured that the exponential rate of change of the norm of H for
large time is constant (almost-sure Lyapunov exponent) and, as the viscosity
increases from zero to a positive value, this rate of change increases very
fast (fast dynamo random generation). An explicit Feynman-Kac-type formula
for H is available, which can be discretized in time and space, offering
theoretical as well as numerical possibilities for tackling this difficult
problem, including using the theory of products of random matrices, and
simulations by particle techniques. ) which
satisfies a linear system of parabolic partial differential equations. If
the velocity field is assumed to be white-noise in time and smooth in space,
then H will satisfy a linear system of three stochastic PDEs, in which the
zero- and first-order terms have coefficients that are white-noise in time.
It is conjectured that the exponential rate of change of the norm of H for
large time is constant (almost-sure Lyapunov exponent) and, as the viscosity
increases from zero to a positive value, this rate of change increases very
fast (fast dynamo random generation). An explicit Feynman-Kac-type formula
for H is available, which can be discretized in time and space, offering
theoretical as well as numerical possibilities for tackling this difficult
problem, including using the theory of products of random matrices, and
simulations by particle techniques.
John Walsh
Stochastic Partial Differential Equations Brownian motion and convergence
rates of binomial tree methods
Abstracts not yet available
Back to Top
|
 |